Lars Vandenbergh's CubeZone

Speedcubing taken one step further

Square-1 solution method - Step 1

Make both layers square

One of the unique and interesting properties of the Square-1 is that it changes shape when you scramble it. Trying to solve the scrambled puzzle without making it into a cube first can prove to be a tough task since a lot of shapes have very limited options to move pieces around. The state where both layers are square is much more manoeuvrable and it allows us to recognise more easily where each piece belongs.

With this method, the long term goal is to be able to make both layers square in the optimal number of twists of the middle layer. But first we're going to investigate the various shapes that one layer can have, and work out which combinations of bottom layer shapes and top layer shapes are possible.

Shapes that one layer can have

A layer can have various combinations of corners (large pieces) and edges (small pieces). There are a few restrictions however. Let's say C is the number of corners and E is the number of edges. Since the inner angle of all pieces must add up to 360°, we know that 60C + 30E = 360 or simpler:

2C + E = 12 (constraint 1)

There are also only 8 small pieces in total and only 8 large pieces in total:

0 <= C <= 8 (constraint 2)
0 <= E <= 8 (constraint 3)

If we consider all possible values for C and calculate the value for E from it using constraint 1, we get the following results:

C=0, E=12
C=1, E=10
C=2, E=8
C=3, E=6
C=4, E=4
C=5, E=2
C=6, E=0
C=7, E=-2
C=8, E=-4

If we discard all possibilities with an invalid value of E using constraint 3, only the following 5 options remain that statisfy all constraints:

2 corners and 8 edges
3 corners and 6 edges
4 corners and 4 edges
5 corners and 2 edges
6 corners and 0 edges

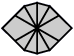
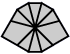
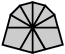
One can now work out all possible arrangements of corners and edges for each subcase, which leads to the following 29 shapes:

2 corners and 8 edges (5 shapes)

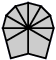4-4	5-3	6-2	7-1	8

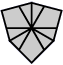
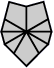
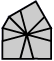
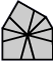
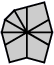
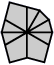
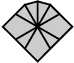
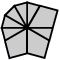
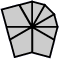
3 corners and 6 edges (10 shapes)

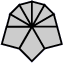2-2-2	3-3	3-2-1	3-1-2	Left 4-2	Right 4-2	4-1-1	Left 5-1	Right 5-1	6

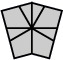
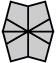
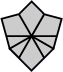
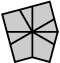
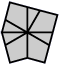
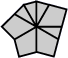
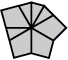
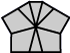
4 corners and 4 edges (10 shapes)

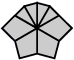Square	Kite	Barrel	Shield	Left fist	Right fist	Left pawn	Right pawn	Mushroom	Scallop

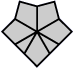
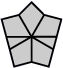
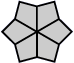
5 corners and 2 edges (3 shapes)			6 corners and 0 edges (1 shape)

Paired edges	Perpendicular edges	Parallel edges	Star

Combining shapes in both layers

Now that we've worked out all possible shapes one layer can have, we can investigate all shapes the whole puzzle can have by considering all possible combinations of 2 shapes (one shape of the top layer and one shape of the bottom layer). Of course, we don't take the state of the middle layer into account. Since the total amount of corners and edges must at all times be exactly 8, we know that:

if the top layer has 6 corners and 0 edges, the bottom layer has to have 2 corners and 8 edges.
if the top layer has 5 corners and 2 edges, the bottom layer has to have 3 corners and 6 edges.
if the top layer has 4 corners and 4 edges, the bottom layer has to have 4 corners and 4 edges.
if the top layer has 3 corners and 6 edges, the bottom layer has to have 5 corners and 2 edges.
if the top layer has 2 corners and 8 edges, the bottom layer has to have 6 corners and 0 edges.

The last two cases in the list contain the same shapes as the first two cases if you put the cube upside down. So from now on we will only talk about 3 possible configurations:

6 corners in the top layer (1 case) and 2 corners in the bottom layer (5 cases) which adds up to 5 cases in total
5 corners in the top layer (3 cases) and 3 corners in the bottom layer (10 cases) which adds up to 30 cases in total
4 corners in the top layer (10 cases) and 4 corners in the bottom layer (10 cases) which adds up to 55 cases in total